Example: Voronoi Hexagonal Tiles

How to go about creating the image above? Did you notice the hexagons hidden in plain sight? The colored fragments do combine to form hexagons. I got this idea to fill a 2-D space with Hexagonal Voronoi polygons. But the journey turned out to be trickier than I originally expected. In this example, I try to recreate my various attempts.

A Voronoi diagram is “the partitioning of a plane with n points into convex polygons such that each polygon contains exactly one generating point and every point in a given polygon is closer to its generating point than to any other.” (Wolfram)

I have always liked Voronoi diagrams. So it was natural that I should try and use them to create Hexagonal tiles. I knew that in Python, this was easily done by using the SciPy module.

The example seemed straightforward to try.

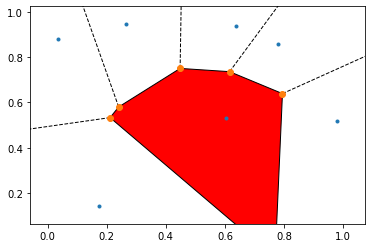
 points = np.random.rand(7,2)
 # compute Voronoi tesselation
 vor = Voronoi(points)

 voronoi_plot_2d(vor, show_vertices = True)

 # colorize
 for region in vor.regions:
     if not -1 in region:
         polygon = [vor.vertices[i] for i in region]
         plt.fill(*zip(*polygon), fc='red')

Now, if we take a few points inside a hexagon, we can then try and divide up the entire hexagon into Voronoi spaces.

 #Generate 10 random points inside a hexagon
 points = []
 for _ in range(10):
     size=0.5
     dist = np.random.random() * size
     theta_offset = np.random.randint(9) * 10
     i = np.random.randint(6)
     points.append( h.get_points_center_rtheta(dist, theta_offset, index=i)[0])

 voronoi_plot_2d(vor, show_vertices = True)
 h.render(fill=None)
 plt.axis('scaled')

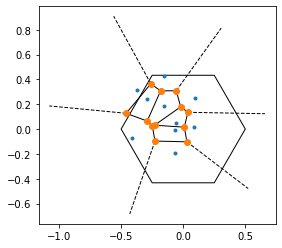
I was able to create Voronoi polygons, but they simply did not fill the space at all.

plt.plot(vor.vertices[:,0],vor.vertices[:,1], 'o', color='orange')

hverts = np.array(h.get_verts())
plt.plot(hverts[:,0], hverts[:, 1], 'b-')
for r in result:
    plt.fill(*zip(*np.array(list(
        zip(r.boundary.coords.xy[0][:-1], r.boundary.coords.xy[1][:-1])))),
        alpha=0.6)
plt.axis('scaled')

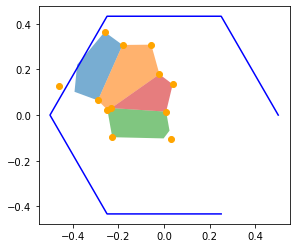
The orange dots in the image above are Voronoi vertices. But as you can see, there a vast part of the Hexagon that is simply not filled. Drawing the region by itself didn’t lead to any insights.

I was stuck in this point for quite some time. More than once, I was ready to give up. But I kept searching to see how others had approached this.

After many more such failed attempts and mishaps, I got an inspiration from this Stackoverflow answer

I noticed that this person was able to take this

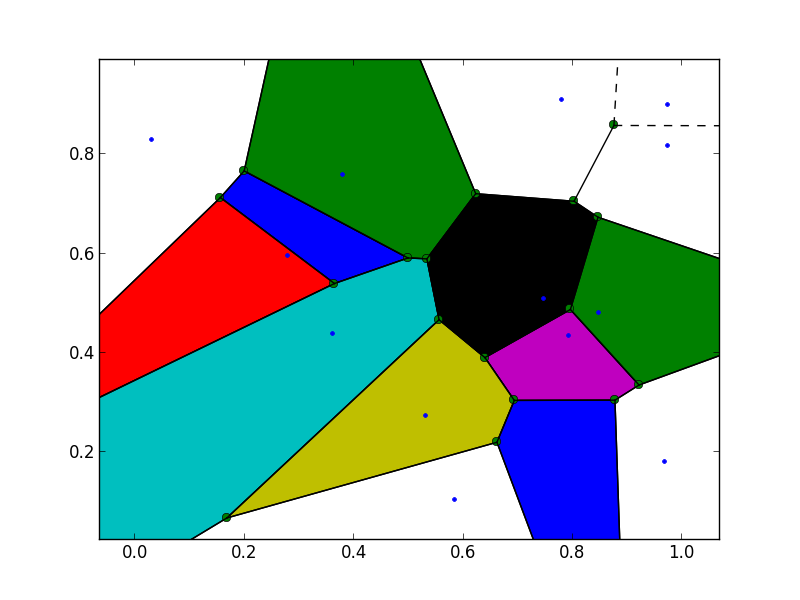
and create this, which is very similar to what I was after.

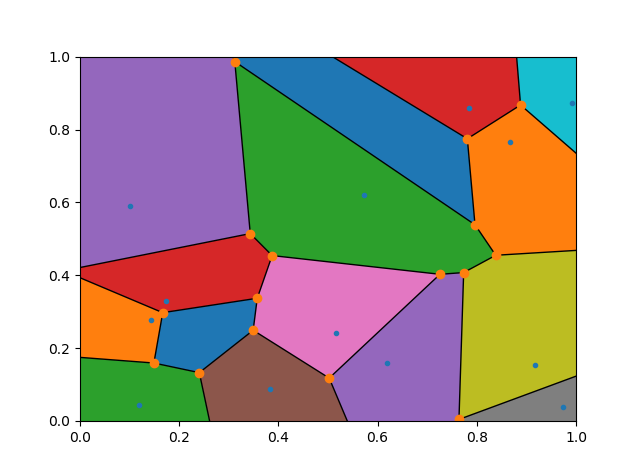
To achieve this, this person had added 4 points well outside the shape of interest. And then by cutting off the x and y limits they got the image they desired.

But my problem is that my base shape is not rectangular. It is a hexagon. After a lot of web searches I figured that an “shape” intersection was the answer. For that, I would have to use the very popular shapely package. Another SO answer really helped me understand how to approach intersecting polygons.

#Adding 6 points well OUTSIDE the Hexagon,
# so that Voronoi will surely cover the entire hexagon
#Doing this so that when intersected with the hexagon mask,
# no part of the original hexagon will be missed
pull_points = h.get_points_center_rtheta(size*4, theta_offset, index=None)
points = np.append(points, pull_points, axis = 0)

Side note: Installing shapely in windows was a bit tricky. But anyway, I finally was getting somewhere.

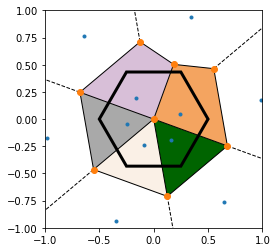
Now, all that remains is to “intersect” my bigger voronoi area and cut out just the hexagon inside it. In order to make sure that I don’t miss any part of the hexagon, my “pull” points are at least 4*size of the hexagon-side away. That seemed to work.

 ridge_lines = [
     LineString(vor.vertices[line])
     for line in vor.ridge_vertices if -1 not in line]

 pts = MultiPoint([Point(i) for i in h.get_verts()])
 hex_mask = pts.convex_hull.union(pts.buffer(0.1, resolution=5, cap_style=2))
 result = MultiPolygon([poly.intersection(hex_mask) for poly in polygonize(ridge_lines)])

Once the idea works for one Hexagon, and it is filled entirely with Voronoi polygons, it was just a matter of choosing the right color palette and putting the pieces together.